![]()
| TU
Kaiserslautern - Fachbereich
Mathematik AG Algebra, Geometrie und Computeralgebra Prof. Dr. W. Decker, Prof. Dr. M. Schulze, Dr. Janko Böhm |
Tel.: +49 (0)631/205-2730 Zi. 435, 434, 430, Geb. 48 D-67663 Kaiserslautern |
decker@mathematik.uni-kl.de mschulze@mathematik.uni-kl.de boehm@mathematik.uni-kl.de |
Seminar: Algorithms in toric and algebraic geometry
Summer Term 2013
![]() The seminar will
be Thursdays, 15:30-17:00 in 48-538. We will begin on 02.05.13.
The seminar will
be Thursdays, 15:30-17:00 in 48-538. We will begin on 02.05.13.
![]() We will have an organizational
meeting on Friday 19.04.13 at 13:45 - 15:15 in 48-538.
We will have an organizational
meeting on Friday 19.04.13 at 13:45 - 15:15 in 48-538.
![]() Please register online in the URM
system.
Please register online in the URM
system.
![]()
The seminar will provide a systematic introduction to toric geometry and
algorithms in toric and algebraic geometry. Toric varieties are special type
of algebraic varieties which are particularly easy to handle. The reason is
that they are described by convex polyhedral objects, from which lots of interesting
information can be obtained in a direct manner (in contrast to an arbitrary
algebraic variety where it is very hard to compute). As an example, the affine
2-dimensional space ![]() 2 can
be represented as a toric variety by the positive orthant with the standard
integer lattice:
2 can
be represented as a toric variety by the positive orthant with the standard
integer lattice:
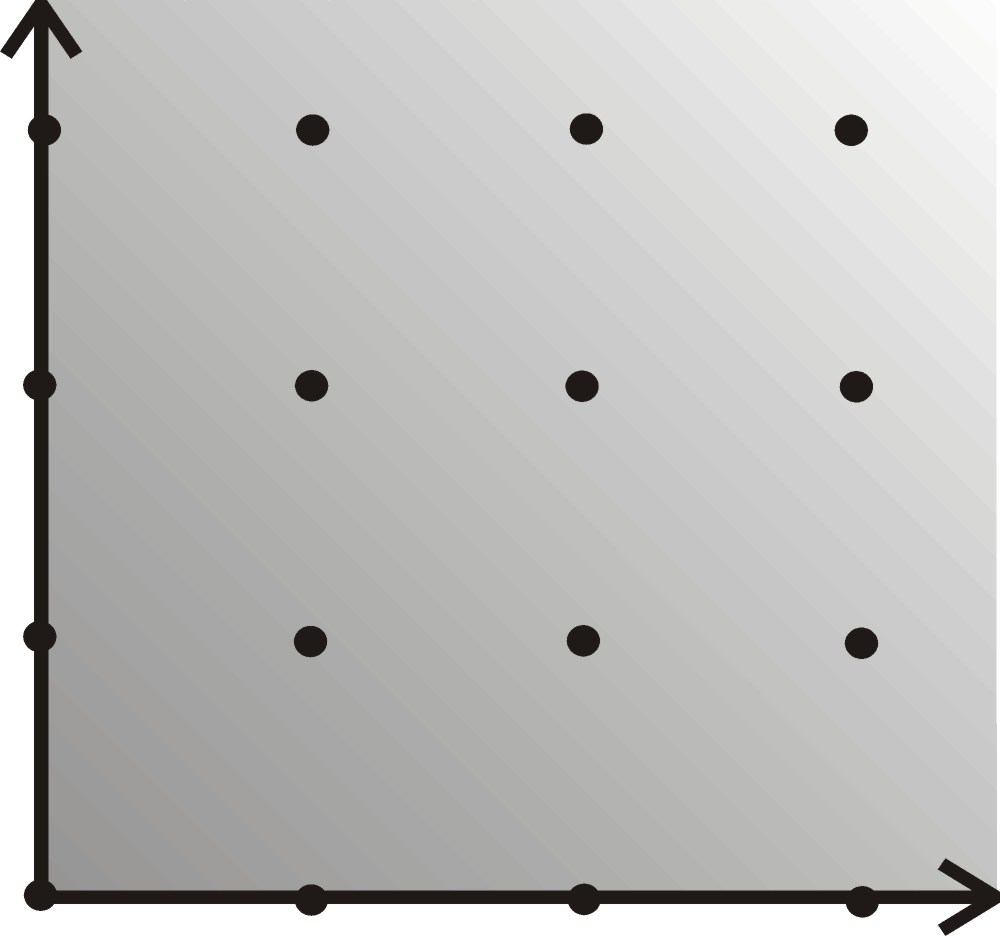
Specifically, we will take a look at the following topics:![]() Convex
polyhedral cones, affine toric varieties (Adrian Koch)
Convex
polyhedral cones, affine toric varieties (Adrian Koch)![]() Projective
toric varieties, fans (Peter Chini)
Projective
toric varieties, fans (Peter Chini)![]() Divisors
(Raul Epure)
Divisors
(Raul Epure)![]() Homogeneous
coordinate rings (Tien Mai Nguyen and Bin Nguyen)
Homogeneous
coordinate rings (Tien Mai Nguyen and Bin Nguyen)![]() Resolution
of singularities
Resolution
of singularities![]() Cohomology
of line bundles (Sasha Valentinova Bagryanova)
Cohomology
of line bundles (Sasha Valentinova Bagryanova)![]() Betti numbers of
toric varieties (Corina Birghila)
Betti numbers of
toric varieties (Corina Birghila)![]() Toric
intersection theory (Hiep Dang).
Toric
intersection theory (Hiep Dang).![]() Riemann-Roch
theorem (Florian Diebold).
Riemann-Roch
theorem (Florian Diebold).![]() Bezout's
theorem (Sebastian Muskalla).
Bezout's
theorem (Sebastian Muskalla).![]() Stanley's
theorem.
Stanley's
theorem.![]() Algebraic
analogues of toric concepts.
Algebraic
analogues of toric concepts.![]() Birational
geometry.
Birational
geometry.
Each participant will give a talk in the seminar. There are topics which
are more theoretical or more practical in nature. The practical ones
come with some implementation work in Singular, which then will be
demonstrated in the talk.
The targeted audience are students who have attended the lecture Computer Algebra or the lecture Commutative Algebra in the winter term, or who are attending the lecture Algebraic Geometry in the current summer term.
However, anyone with a basic knowledge of commutative algebra is welcome. Knowledge in algebraic geometry is not required.
The seminar is a good starting point if you plan to write any sort of thesis in computer algebra or algebraic geometry.
|
W. Fulton |
Princeton University Press |
1993 |
ISBN 978-0-691-00049-7 | |
D. A. Cox, J. Little, H. Schenck |
AMS |
2010 |
ISBN 978-0-821-84819-7 |
|
| G.-M. Greuel, G. Pfister | A SINGULAR Introduction to Commutative Algebra | Springer | 2002 | ISBN 978-3-540-73541-0 |
| D. A. Cox, J. Little, D. O'Shea |
Springer | 2007 |
ISBN 978-0-387-35650-1 |
|
| H. Schenck |
Cambridge University Press | 2003 |
ISBN 978-0-521-53650-9 |
|
| W. Decker, Ch. Lossen |
Computing in Algebraic Geometry - A Quick Start using Singular | Springer | 2005 |
ISBN 978-3-540-28992-0 |
|
W. Decker, G. Pfister |
A First Course in Computational Algebraic Geometry | Cambridge University Press |
2012 |
in print |
Module description for the Bachelor courses in Mathematics.
![]() 2 SWS seminar
2 SWS seminar![]() 3 credit
points
3 credit
points
![]() 30h contact
hours for the seminar
30h contact
hours for the seminar![]() 60h
self-study hours
60h
self-study hours
The seminar will be Thursdays, 15:30 - 17:00 in 48-538.
We will begin on 02.05.13.
Please register online in the URM
system. Write an email to boehm@mathematik.uni-kl.de
if you have any issues with the date.
There will be organizational meeting in the first week of the semester.
![]()
Anyone is wellcome to listen to the seminar. To obtain credit points you will have to give a talk.
Singular:
The open source computer algebra system Singular is being developed in Kaiserslautern. It is one of the leading systems for calculations in polynomial rings. Algorithms implemented in Singular deal with Gröbner bases, free resolutions, polynomial factorization, primary decomposition, and many other problems in commutative algebra.
You can download Singular here, read the online manual is here, and obtain the source code here.
Polymake:
The open source computer algebra system Polymake is one of the leading systems for calculations in convex geometry. It has facilities for visualization and can be accessed directly from Singular.
You can download Polymake here, read the online manual is here.
![]()
| |
| Prof.
Dr. Wolfram Decker Zi. 434, Geb. 48 D-67663 Kaiserslautern Tel.: +49 (0)631/205-5489 decker@mathematik.uni-kl.de |
| Prof.
Dr. Mathias Schulze Zi. 434, Geb. 48 D-67663 Kaiserslautern Tel.: +49 (0)631/205-5489 mschulze@mathematik.uni-kl.de |
| Dr. Janko
Böhm Zi. 430, Geb. 48 D-67663 Kaiserslautern Tel.: +49 (0)631/205-2730 boehm@mathematik.uni-kl.de |
![]()